Polynomial Regression

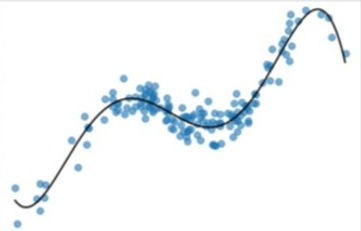
Introduction and Background

Polynomial regression is a method of approximating the relationship of a dataset with some degree polynomial. Polynomial regression can be viewed as a special case of multiple linear regression. For a set of m inputs we aim to find a polynomial of degree k of the following form

such that the sum of square errors is minimized. A quick derivation can be seen below.

Examples

- Creating a Dataset

The first thing you will need is a dataset that will be used to compute the polynomial regression model. We create two arrays, x and y, which will be the features and targets respectively for the polynomial regression model. The x array contains a single input for the polynomial. These arrays can hold any data you want but for this example we will stick with just a few simple numbers.

- Defining and Fitting the Model

We can now define our model by creating a PolynomialRegression object. In this example we name the multiple linear regression model "polyReg" but you can name it anything you want. Once the model has been defined we can "fit" the model to our dataset. This is the step that actually computes the line and finds the optimal parameters. The constructor takes an optimal integer parameter for the degree of the polynomial to fit to the data. If no value is given, then it will default to a line and will be equivalent to linear regression.

- Inspecting the Fit Model

If you want to view the details of the model, including the computed parameters of the polynomial, you can call model_name.inspect(). Below you can see the code for this and the resulting output.

- Making Predictions

Now that the polynomial regression model has been fit, we can feed in new data and see what the model predicts the output to be. First, lets define a new array called test that contains the data we want to make predictions on.